一年级数学教学14:数图形
文 | 谆仪
在一年级数学中,会要求孩子数出给出的图形中的特定形状的数量。在这一类的题中,所有的图形不再是完全分开的,而是大大小小地图形合在一起,图中有图。比如,我们常见的数三角形的题,如下图所示:
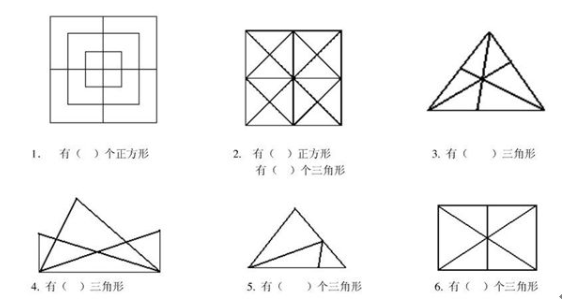
在数图形教学中,需要孩子具备的前备技能是1)区辨不同的图形,包括平面图形和立体图形;2)点数报总数;3)在干扰条件下区辨图形并数出数量(干扰条件包括a. 图形中包含其它东西,而不仅是简单线条的图形;b. 给出的图中包括多种图形)。
下面,我们会通过一些常见题型来讨论教导的要点:
例题1:下图中有多少个长方形?

对于孩子来讲,找出独立的图形并不困难,难点在于找出包含有小图形的大图形。在受视觉干扰的条件下,孩子经常会漏掉一些隐藏在其中的形状。所以,教导的重点在于1)找出隐藏的大图形;2)通过标记来帮助孩子记住哪些图形已经找过了,哪些还没有。
教导程序:
-
家长展示要数的图形在孩子面前,指示孩子读题
-
家长先让孩子自己找一找。
在这一步,孩子应该能找出最直观的小图形,家长要求孩子用同一种颜色的笔将图形标记出来。如下图所示:
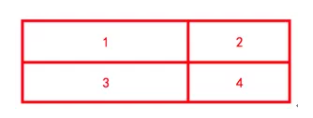
3. 家长通过示范来教导孩子找出隐藏的大的长方形,使用不同的颜色笔来加强视觉效果,如下图所示:
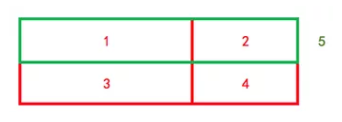
家长让孩子尝试找出类似的长方形,如果孩子无法找到,家长再示范,如下图所示:
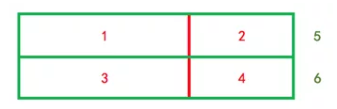
4. 家长再让孩子以相同的规律找出其它的长方形,如上一步,如果孩子无法找出(比如:孩子持续寻找的时间达到30秒-1分钟,或by孩子求助),家长给出示范。每一次示范后,家长都会让孩子再尝试自己寻找。在练习一几道题后,家长也可以通过给出提示的方法来逐渐撤销示范辅助,比如用手遮掉一半的图形,或用手指描画图形。每次给出辅助,都给予孩子一定的思考时间,如果孩子在思考20-30秒后仍然无法解答,家长需要进一步给出辅助。
本题后续的解题步骤如下:
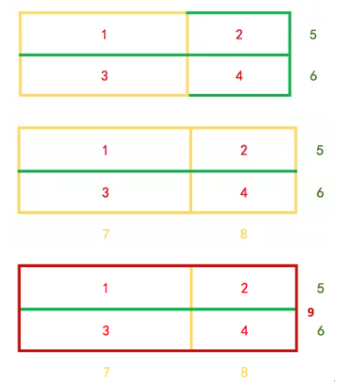
5. 家长提问孩子一共有多少长方形
家长可以根据标记下的数字直接回答:“9个”;在这一步,家长可以要求孩子再一次数出所有的9个长方形,在数的时候,用手指描画长方形的外框。(注:在我们给出的图形示范中并没有保留前面步骤中画的颜色,所以不直观;但在现实生活中,孩子是用手描绘的,所以不同颜色的外框会留在图形上,会方便孩子重新点数。)
6. 家长要求孩子将答案写在题目要求的位置。
7. 当孩子完成解答后,家长夸奖孩子
8. 给出下一题,让孩子继续练习。每次训练建议练习5道题左右。
注意:在数这类图形时要避免的就是不遗漏,但也不能重复,所以家长要教导孩子按照一定的顺序去数,可以从里面数到外面(也就是先数小的,再数大的),也可以从外面数到里面(也就是先数最大的,再数小的),不论哪一种数法,最好让孩子每数出一个形状就用笔标记出来,标记的方式可以是描出该图形的边框,也可以在图形内画不同的线条来标记,也可以用数字来标记。
例题2:数出下图中的正方体个数
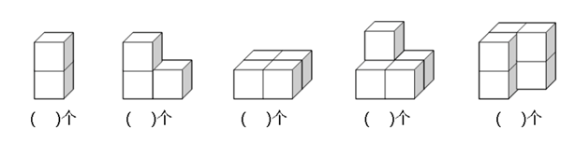
在早期的训练中,我们会进行【积木仿搭】的训练,该技能会为解立体数图形的题目做一定的铺垫。积木仿搭包括以下目标阶段:
1) 跟随仿搭,即家长搭一块,孩子搭一块
2) 整体仿搭:即根据给出的图形进行仿搭,包括3D立体图形和2D平面图形(通常会先教导3D的仿搭,但根据孩子的学习特点,如果发现孩子更易于跟随2D图来仿搭,也不仿可以从2D开始教导)
前两个阶段一般使用方形积木块(或少数几种形状的积木块)来进行训练,教导的重点在于a. 根据形状颜色来选择正确的积木;b. 将积木按示范搭放在正确的位置。
3) 搭乐高积木:在练习时,积木数量越来越多,图形也越来越复杂,直至最后孩子可以拿到整套的积木,按说明书完成拼搭。
当孩子具有这个能力时,孩子应该已经注意到,有些积木在眼前是看不到的。在训练的时候,我们会观察到,孩子会探头到给出的3D示范的背面去看正面看不到的积木的颜色或形状。
立体图形的题的难点在于:要将看不到的图形数进去,所以,教导的关键点在于让孩子意识到有看不到的图形。当然,解题仍然是有技巧的。与数平面图形类似,在数立体图形时,我们仍然要有顺序地去数,一般会按层,从完全看得见的层面开始数,然后按顺序一层一层往下数。以下题为例:
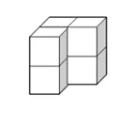
教导程序:
1. 家长展示题目在孩子面前,指示孩子:数一数一共有几个正方体?
2. 家长提问孩子一共有几层?
如果孩子不能回答,家长用手势指出,或用颜色笔在两层之间划出界限,指出一共有2层。
3. 家长要求孩子先数看得到的一层,即最上面的一层。
孩子数出有3块(一般情况下,孩子可以完成这一步)
4. 家长要求孩子数第2层
家长需要指出,第2层与第1层是完成重合的,所以是一模一样的。如果孩子不能理解,家长可以使用积木来演示给孩子看。
5. 当孩子数出第2层也有3块积木,家长要求孩子将两层的积木数量相加,或让孩子从头开始再数一次,最终得出一共有6块积木的答案。
6. 家长要求孩子按照题目要求将答案写在对应的位置
7. 家长夸奖孩子做对了
8. 变化下一题进行练习,建议每次训练做5题左右
例题3:多种形状的组合图形
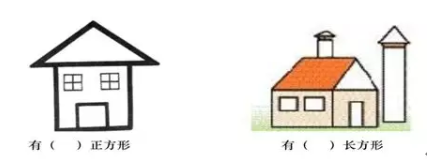
在这类题中不再是单一的图形,而是一个题中会有多种图形,而让孩子去数出指定的图形。这一类题在数形状上并没有太大的难点,关键点在于(1)能在干扰下数特定形状;(2)能无遗漏地找出复合图形中所有的特定形状,所以标记仍然会是一个有用的方法。
教导程序:
1. 家长指示孩子读题
2. 找出问题的关键词:家长提问孩子,要数什么形状?
孩子需要能回答“正方形”
3. 家长指示孩子找出图中的正方形,并做上标记(可以使用彩笔)
· 当孩子有所遗漏时,家长可以给出提示,提示的方法包括a. 口语(如:门是什么形状?);b. 手势(家长用手指或描画孩子未数出的正方形,如房子);c. 家长用采笔勾画出正方形。
· 图中如果有复合图形(如窗户),教导方法见例题1
· 每数出一个图形,可让孩子用数字做出标记以免漏数
· 观察时,帮助孩子养成同一方向(从上向下、从左往右)查找的习惯
4. 当孩子数出正确的个数时,家长指示孩子把答案写在题目要求的对应位置
5. 家长夸奖孩子
6. 家长给出下一题(建议每次练习不超过5题)
例题4:数缺失的图形数量
一面单层的砖墙下暴雨时塌了,少了一些砖(如下图)。请你帮忙计算一下,需要多少块砖才能把墙补好。
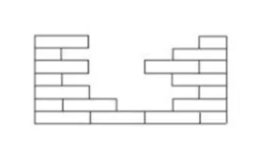
这一类题,因为要数的是缺失的部分,所以孩子没有办法直接进行点数。解题可以从两个方向着手:(1)将缺失的墙面补齐;(2)找规律后进行计算。
方法1比较花时间,而且孩子需要有能力进行绘画,当然,在完成绘画后,点数的过程会很容易。
方法2节省时间,并且有可泛化性,所以我们会建议家长教导孩子如何寻找规律,最终通过计算来得出结果。
教导程序:
1. 家长要求孩子读题,并且指出要点数的是看不到的部分的长方形的数量。
如果孩子完全无法理解,家长可以遮掉一部分的图形,简化题目来帮助孩子理解,如下图所示。
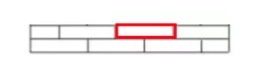
2. 找规律:家长提示孩子找出完整的一层墙面,即最底层,并且要求孩子数出一共有多少块砖。
规律为:3块大砖,1块小砖
3. 家长要求孩子逐层数出有多少砖,并且计算出缺了多少块砖(如下图所示)
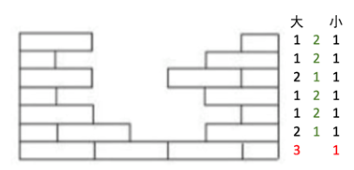
在点数过程中,我们会发现,小砖并没有缺少,而每一层都少了大砖。根据每层应该有3块大砖,要求孩子在每一层写下缺少的砖的数量。
4. 计算:家长指示孩子计算缺少的砖的总数量:2+2+1+2+2+1=10
5. 家长指示孩子把答案写在题目要求的对应位置
6. 家长夸奖孩子
7. 家长给出下一题(建议每次练习不超过5题)